Understanding Kolmogorov–Arnold Networks (KAN)
Why KANs are a potential alternative to MPLs and the current landscape of Machine Learning. Let’s go through the paper to find out.
Anew research paper titled KAN: Kolmogorov–Arnold Network has stirred excitement in the Machine Learning community. It presents a fresh perspective on Neural Networks and suggests a possible alternative to Multi-Layer Perceptrons (MLPs), a cornerstone of current Machine Learning.
Inspired by the Kolmogorov-Arnold representation theorem, KANs diverge from traditional Multi-Layer Perceptrons (MLPs) by replacing fixed activation functions with learnable functions, effectively eliminating the need for linear weight matrices.
I strongly recommend reading through this paper if you’re interested in the finer details and experiments. However, if you prefer a concise introduction, I’ve prepared this article to explain the essentials of KANs.
Note: The source of the images/figures used in this article is the “KAN: Kolmogorov–Arnold Network” paper unless stated otherwise.
The Theory
The theoretical pillar of these new networks is a theory developed by two Soviet mathematicians, Vladimir Arnold and Andrey Kolmogorov.
While a student of Andrey Kolmogorov at Moscow State University and still a teenager, Arnold showed in 1957 that any continuous function of several variables can be constructed with a finite number of two-variable functions, thereby solving Hilbert’s thirteenth problem. (source: Wikipedia)
The theory that they worked on and eventually developed was based on the concept of multivariate continuous functions. According to this theory, any multivariate continuous function f can be written as a finite composition of continuous functions of a single variable, summed together.

How Does This Theorem Fit into Machine Learning?
In machine learning, the ability to efficiently and accurately approximate complex functions is an important subject, especially as the dimensionality of data increases. Current mainstream models such as Multi-Layer Perceptrons (MLPs) often struggle with high-dimensional data — a phenomenon known as the curse of dimensionality.
The Kolmogorov-Arnold theorem, however, provides a theoretical foundation for building networks (like KANs) that can overcome this challenge.
How can KAN avoid the curse of dimensionality?
This theorem allows for the decomposition of complex high-dimensional functions into compositions of simpler one-dimensional functions. By focusing on optimizing these one-dimensional functions rather than the entire multivariate space, KANs reduce the complexity and the number of parameters needed to achieve accurate modeling. Furthermore, Because of working with simpler one-dimensional functions, KANs can be simple and interpretable models.
What Are Kolmogorov–Arnold Networks (KAN)?
Kolmogorov-Arnold Networks, a.k.a KANs, is a type of neural network architecture inspired by the Kolmogorov-Arnold representation theorem. Unlike traditional neural networks that use fixed activation functions, KANs employ learnable activation functions on the edges of the network. This allows every weight parameter in a KAN to be replaced by a univariate function, typically parameterized as a spline, making them highly flexible and capable of modeling complex functions with potentially fewer parameters and enhanced interpretability.
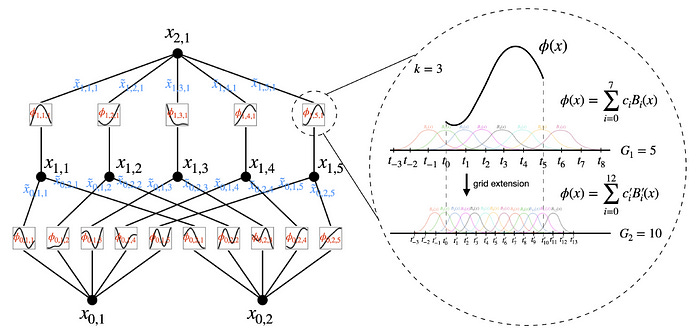
KAN architecture
The architecture of Kolmogorov-Arnold Networks (KANs) revolves around a novel concept where traditional weight parameters are replaced by univariate function parameters on the edges of the network. Each node in a KAN sums up these function outputs without applying any nonlinear transformations, in contrast with MLPs that include linear transformations followed by nonlinear activation functions.
B-Splines: The Core of KAN
Surprisingly, one of the most important figures in the paper can be missed easily. It’s the description of Splines. Splines are the backbone of KAN’s learning mechanism. They replace the traditional weight parameters typically found in neural networks.
The flexibility of splines allows them to adaptively model complex relationships in the data by adjusting their shape to minimize approximation error, therefore, enhancing the network’s capability to learn subtle patterns from high-dimensional datasets.
The general formula for a spline in the context of KANs can be expressed using B-splines as follows:
Here, 𝑠pline(𝑥) represents the spline function. ci are the coefficients that are optimized during training, and 𝐵𝑖(𝑥) are the B-spline basis functions defined over a grid. The grid points define the intervals where each basis function 𝐵𝑖 is active and significantly affects the shape and smoothness of the spline. You can think of them as a hyperparameter that affects the accuracy of the network. More grids mean more control and precision, also resulting in more parameters to learn.

During training, the ci parameters of these splines (the coefficients of the basis functions Bi(x) ) are optimized to minimize the loss function, thus adjusting the shape of the spline to best fit the training data. This optimization often involves techniques like gradient descent, where each iteration updates the spline parameters to reduce prediction error.
The Best of Two Worlds
While KAN is based on the Kolmogorov-Arnold representation theorem, it is just as inspired by MLPs, “leveraging their respective strengths and avoiding their respective weaknesses”. KAN benefits the structure of MLP on the outside, and splines on the inside.
As a result, KANs can not only learn features (thanks to their external similarity to MLPs), but can also optimize these learned features to great accuracy (thanks to their internal similarity to splines).
Network Simplification
The paper goes on to explain some methods to simplify the network and our interpretation of them. I will only proceed to refer to two of them which were fascinating to me.
Symbolification: KAN is constructed by approximating functions using compositions of simpler, often interpretable functions. This results in their unique ability to hand over interpretable mathematical formulas, such as shown in the figure above.
Pruning: The other aspect of KANs discussed in the paper is about optimizing the network architecture by removing less important nodes or connections after the network has been trained. This process helps in reducing the complexity and size. Pruning focuses on identifying and eliminating those parts of the network that contribute minimally to the output. This makes the network lighter and potentially more interpretable.
Is KAN New?
Kolmogorov-Arnold representation theorem is not new, so why has the practice of using it in machine learning not been studied before? As the paper explains, multiple attempts have been made…
However, most work has stuck with the original depth-2 width-(2n + 1) representation, and did not have the chance to leverage more modern techniques (e.g., back propagation) to train the networks.
The novelty of the paper is to adapt this idea and apply it to the current landscape of ML. Using arbitrary network architecture (depth, width) and employing techniques such as backpropagation and pruning, KAN is closer to practical use cases than previous studies.
the Kolmogorov-Arnold representation theorem was basically sentenced to death in machine learning, regarded as theoretically sound but practically useless.
So even though there have been attempts to use Kolmogorov-Arnold representation theorem in ML, it’s fair to say KAN is a novel approach in that it is aware of where ML stands today. It’s a good update to an idea explored before on a limited scale.
4 Fascinating Examples
The paper compares KAN and MLP on several criteria, most of which are gripping. In this part, I will proceed to list some of these interesting examples. The full details of these examples and more are in the paper.
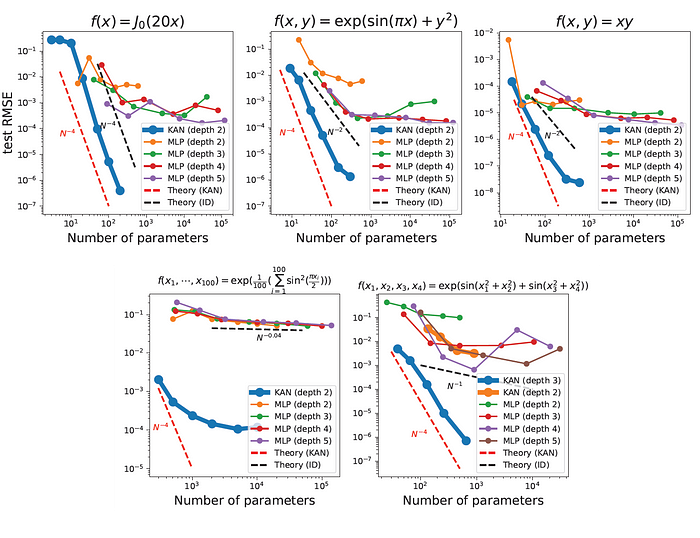
Fitting Symbolic Formulas
This is an example of training various MLPs and a KAN to fit certain functions of various input dimensions. As can be seen below, KAN has much better scalability compared to MLPs (at least in this range of parameter numbers).
This highlights the greater expressive power of deeper KANs, which is the same for MLPs: deeper MLPs have more expressive power than shallower ones.
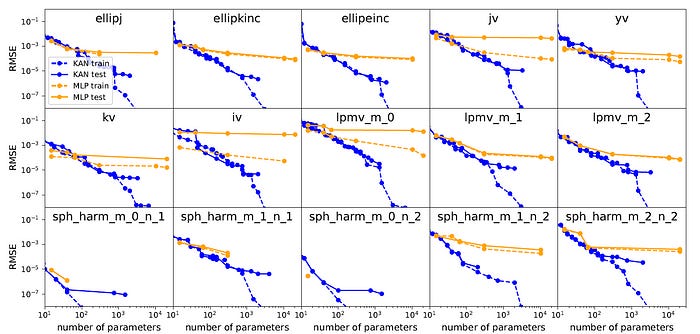
Special Functions
Another example in the paper is to compare KAN and MLP on fitting 15 special functions common in math and physics. The result shows that in almost all of these functions, KANs achieve a lower train/test loss having the same number of parameters compared to MLPs.
Continual Learning
Continual Learning is the quality of how networks can adapt to new information over time without forgetting previously learned knowledge. It is a significant challenge in neural network training, particularly in avoiding the problem of catastrophic forgetting, where acquiring new knowledge leads to a rapid erosion of previously established information.
KANs demonstrate an ability to retain learned information and adapt to new data without catastrophic forgetting, thanks to the local nature of spline functions. Unlike MLPs, which rely on global activations that might unintentionally affect distant parts of the model, KANs modify only a limited set of nearby spline coefficients with each new sample. This focused adjustment preserves previously stored information in other parts of the spline.
Partial Differential Equation solving
PDE solving, a 2-Layer width-10 KAN is 100 times more accurate than a 4-Layer width-100 MLP (10−7 vs 10−5 MSE) and 100 times more parameter efficient (102 vs 104 parameters).
The paper continues to present more experiments. One of them includes applying KANs to the problem of geometric knot invariant, achieving 81.6% test accuracy with a 200-parameter KAN, while an MLP model by Google Deepmind achieves 78% having ~ 3 * 10⁵ parameters. This experiment was performed on the
Final Thoughts
Is the hype over KAN worth it?
It depends on your perspective. The reason KAN is being discussed so far is that it’s a potential light at the end of the ML tunnel. I have discussed in “AI Is Hitting A Hard Ceiling It Can’t Pass” how we need fresh innovations to guide us through the future barriers of Machine Learning, namely Data and Computation. KANs, though not intentionally, can be a way out.
KAN is written with scientific applications of AI in mind, but already people are using it to mix various ML cocktails, including Multihead Attention.
KAN + LLM?
The paper focuses mainly on the AI + Science applications of Kolmogorov-Arnold Networks due to their ability to model and discover complex scientific laws and patterns effectively. KANs are particularly suited for tasks that require the understanding and interpreting of underlying physical principles, as their structure allows for the decomposition of functions into symbolic mathematical expressions. This makes them ideal for scientific research where discovering such relationships is crucial, unlike in large language models (LLMs) where the primary goal often revolves around processing a mammoth corpus of data for natural language understanding and generation.
Author’s Notes
I encourage you to also read the author’s notes on the GitHub page. It provides perspective on what KAN was aimed for, and what could be in the future.
The most common question I’ve been asked lately is whether KANs will be next-gen LLMs. I don’t have good intuition about this. KANs are designed for applications where one cares about high accuracy and/or interpretability. We do care about LLM interpretability for sure, but interpretability can mean wildly different things for LLM and for science. Do we care about high accuracy for LLMs? I don’t know, scaling laws seem to imply so, but probably not too high precision. Also, accuracy can also mean different things for LLM and for science. This subtlety makes it hard to directly transfer conclusions in our paper to LLMs, or machine learning tasks in general.
Conclusion
In my view, it’s best to look at KAN for what it is, rather than what we like it to be. This doesn’t mean KAN is impossible to be integrated within LLMs, already there is an efficient PyTorch implementation of KAN. But it has to be noted, it is too soon to call KAN revolutionary or game-changing. KAN simply needs more experiments done by community experts.
While KANs offer significant advantages in certain contexts, they come with limitations and considerations that beget caution:
Complexity and Overfitting: KANs can potentially overfit, especially in scenarios with limited data. Their ability to form complex models might capture noise as significant patterns, leading to poor generalization.
Computation: KANs may face challenges with GPU optimization due to their specialized nature, which can disrupt parallel processing. This architecture could result in slower operations on GPUs, necessitating serialization and leading to inefficient memory utilization, potentially making CPUs a more suitable platform for these networks.
Applicability: KANs are primarily designed for scientific and engineering tasks where understanding the underlying function is crucial. They might not be as effective in domains requiring large-scale pattern recognition or classification, such as image recognition or natural language processing, where simpler or more abstract models might suffice.
I have to add this has been an amazing paper to read. It’s always exciting to think outside the box and KAN certainly achieves that.
💬 How do you see the potential of KAN? Is it going to niche down to science, or play a key role in our daily AI products?
🌟 Join +1000 people learning about
Python🐍, ML/MLOps/AI🤖, Data Science📈, and LLM 🗯
follow me and check out my X/Twitter, where I keep you updated Daily:
Thanks for reading,
— Hesam













This post doesn't say anything about identification technique. The referred article uses Broyden method and this is why it is slow. There are other approaches. One of them uses Kaczmarz method is much more effective https://www.sciencedirect.com/science/article/abs/pii/S0952197620303742
The coding example can be found in http://openkan.org/DLpiecewiseCPP.html
The dataset 10 000 records, 5 features needs only 0.1 second. MIT paper Python example needs 23 seconds for 2000 records and 2 features.